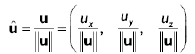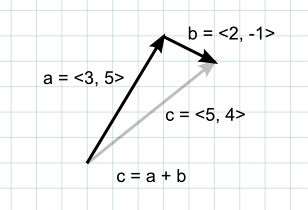虽然游戏引擎已经为我们提供了很多方便的向量运算接口,但一些基础知识还是要掌握了,否则就不知道该找什么接口。大多知识是高中数学里的,所以更详细的可以去找教材。概念性的东西应该记住,具体的运算方式知道就行,需要的时候再来查。
向量与标量
向量:既有大小,又有方向。
标量:只有大小。
零向量:长度为0的向量。
单位向量:长度为1的向量。
平行向量(共线向量):方向相同或相反的非零向量。任意一组平行向量都可以移到同一直线上。零向量与所有向量平行。
相等向量:大小相等且方向相同的向量。相等向量经过平移后总可以重合。
向量的模
向量的模指的是向量的大小(或长度)。
2D向量(x,y),模长是:![]()
3D向量(x,y,z),其中x,y,z分别是三轴上的坐标,模长是:![]()
单位化(标准化)向量
单位化(标准化)向量,就是将向量的大小(模)变为1。
一个向量除以它的模,得到单位向量。
2D向量标准化: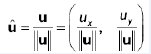
加法
a+b等于使b的始点与a的终点重合时,以a的始点为始点,以b的终点为终点的向量。
- a+b=(x+x’, y+y’)
- 交换律:a+b=b+a
- 结合律:(a+b)+c=a+(b+c)
- 如果将第一个向量当作空间中的一个点,那么,第二个向量可理解为从该位置的位移或“跳跃”。例如,要在地面某位置找到一个单位大于 5 的点,可以使用以下方式进行计算:var pointInAir =pointOnGround + new Vector3(0, 5, 0);
- 如果向量代表力,则更为直观的理解方式是,将其视为含有各自方向和量值的力(量值是指力的大小)。将两个力向量相加所得的新向量即为两者力之和。通常,此概念在计算由多个分力同时作用的力时很有用(例如向前推进的火箭可能会受到侧风的影响)。
减法
a-b等于使b的始点与a的始点重合时,以b的终点为始点,以a的终点为终点的向量。
- a-b=(x-x’, y-y’)
- 不满足交换律,即:a-b≠b-a
点积
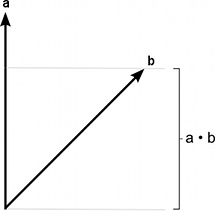
点积(内积、点乘、数量积)是将两个向量相乘得出一个标量的运算。此标量等于两个向量量值相乘的结果再乘以两个向量形成的角度的余弦值。
余弦值
两个向量都为单位向量时,余弦值实际上就是第一个向量在第二个向量上的射影长度(或反之亦然– 参数顺序不会影响结果)。它的几何意义就是a的长度与b在a上的投影长度的乘积,或者是b的长度与a在b上投影长的乘积,它是一个标量,而且可正可负。
- a·b=|a|·|b|·cos<a,b>
- (λa)·b=λ(a·b)
- a·a=|a|的平方
- a⊥b 〈=〉a·b=0
- a·b=x·x’+y·y’
- 交换律:a·b=b·a
- 分配率:(a+b)·c=a·c+b·c
- 不满足结合律,即:(a·b)·c≠a·(b·c)
- 如果AB = 0,那么向量A和B垂直A⊥B
- 如果AB < 0,那么向量A和B之间的夹角α > 90°
- 如果AB > 0,那么向量A和B之间的夹角α < 90°
叉积
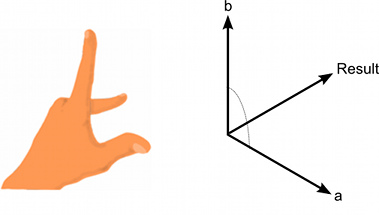
叉积(外积、矢积、叉乘)的结果仍是一个垂直于两个输入向量的向量。
叉积仅适用于三维向量,它输入两个向量,返回另外一个向量作为结果。
结果向量的量值等于两个输入向量量值相乘的结果再乘以两个向量形成角度的正弦值。
“左手坐标系”可用于根据输入向量的顺序表示输出向量的方向。如果第一个参数指向大拇指方向,第二个参数指向食指方向,则结果将指向中指方向。如果参数顺序相反,则结果向量将指向完全相反的方向,但其量值相同。
- A = [x, y, z] B = [x, y, z]
- A×B =[AyBz – AzBy, AzBx – AxBz, AxBy – AyBx]
- (λa)×b=λ(a×b)=a×(λb)
- 分配律:a×(b+c)=a×b+a×c
- 不满足交换律,即:a×b ≠ b×a,实际为a×b = -b×a
- ∣a×b∣是以a和b为边的平行四边形面积
- a×a=0
- a垂直b〈=〉a×b=0
- 向量没有除法,即“a/b”是没有意义的。
平面法线
任何两个3D向量都可以确定一个平面,而平面法线就是一个垂直于该平面的向量,而且其长度为1。
平面法线 = (AB) / (||AB||),其实就是对AB进行的标准化后得到的一个模为1的向量。